シミュレーションで使うなめらかなパルス波形まとめ

投稿日： 更新日:

シミュレーションでパルス（0→1→0）の信号を入れるとき、立ち上がりと立ち下がりをどう表現するかを調べていたのでそれについて備忘録としてまとめました。

記号

  • tont_\mathrm{on} : 立ち上がり開始時刻
  • tofft_\mathrm{off} : 立ち下がり開始時刻
  • triset_\mathrm{rise} : 立ち上がり時間（0→1へ変化するまでの時間）
  • tfallt_\mathrm{fall} : 立ち上がり時間（1→0へ変化するまでの時間）

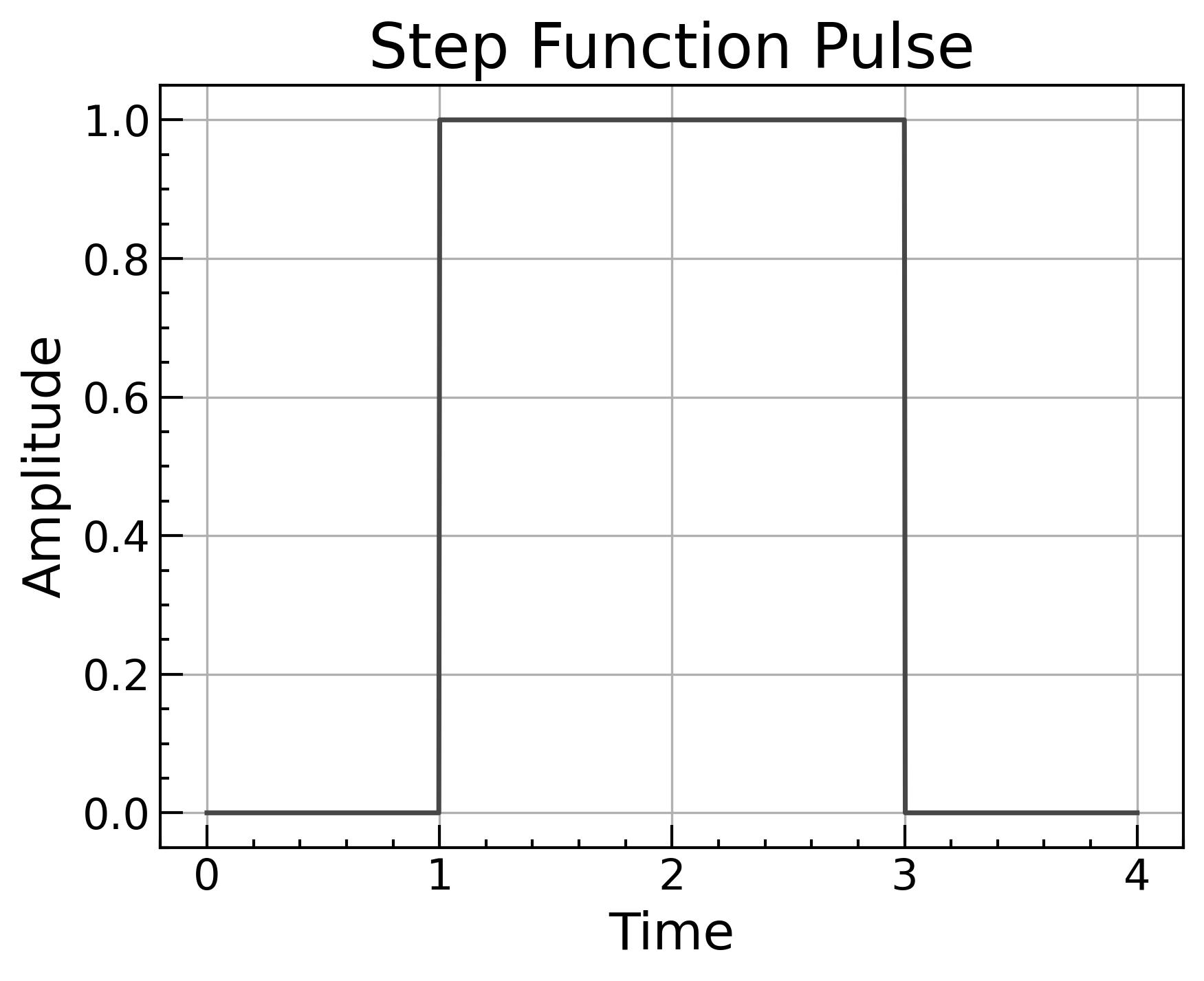
1. ステップ関数型

f(t)={1ton≦t<toff0otherwise.f(t) = \begin{cases} 1 & t_\mathrm{on} \leqq t < t_\mathrm{off} \\ 0 & \text{otherwise.} \end{cases}

とても簡単ですが、立ち上がり・立ち下がり時間が0なので予期しない高周波成分の原因になりシミュレーションが不安定になります。 実装が簡単で便利ですがもう少し丁寧にしたいです。

def step_func_pulse(t, t_on, t_off):
    if t_on <= t < t_off:
        return 1
    return 0

最もシンプルな実装ですがこれには立ち上がり時間、立ち上がり時間を考慮していないという課題があります。 実際のパルスは立ち上がり、立ち上がり時間が存在します。

ステップ関数でのパルス

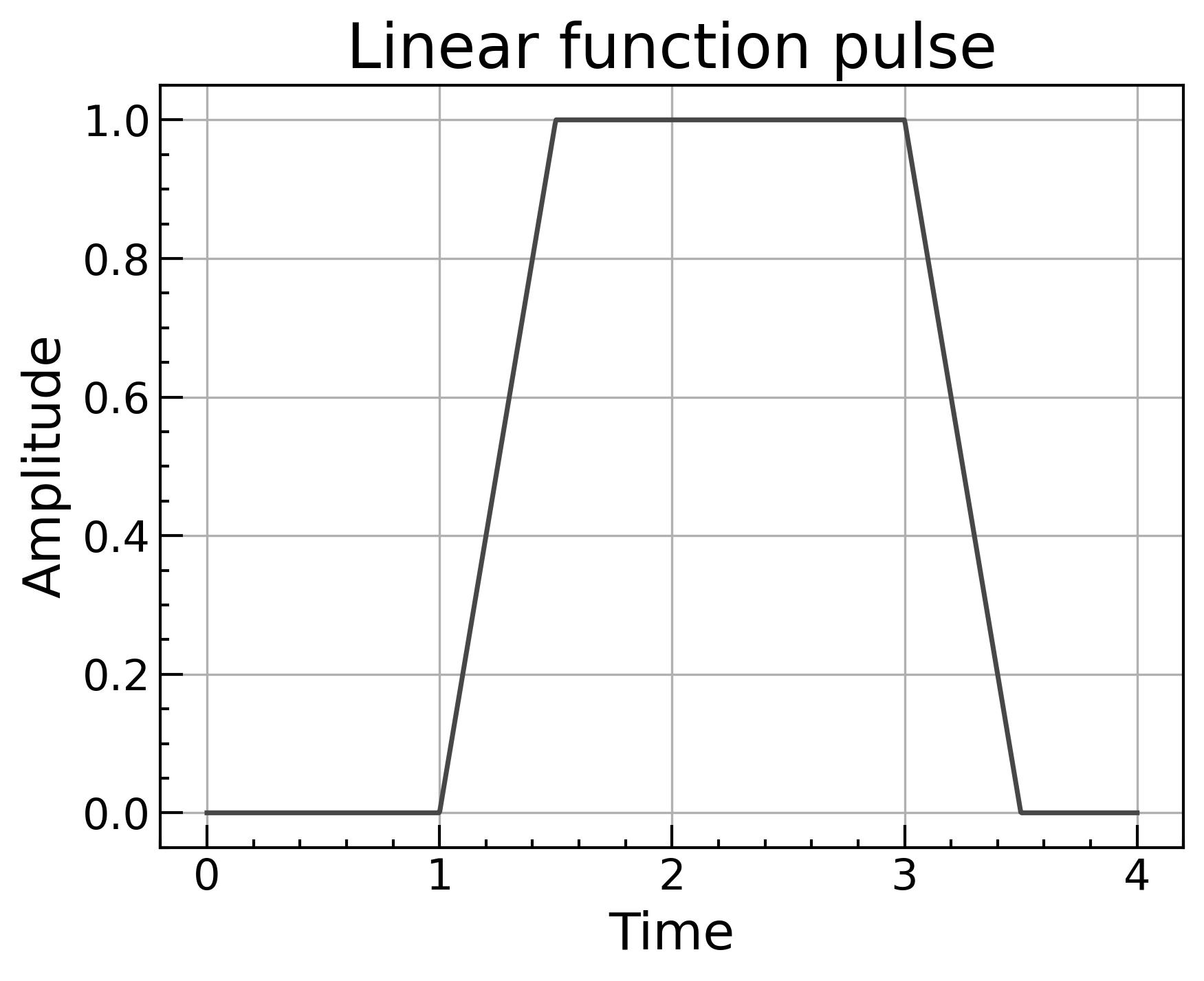
2. 線形ランプ

立ち上がりと立ち下がりを時間に対して直線でつなぐ方法です。

f(t)rise=t−tontrisef(t)fall=1−t−tofftfall\begin{align*} f(t)_\mathrm{rise} &= \frac{t - t_\mathrm{on}}{t_\mathrm{rise}} \\ f(t)_\mathrm{fall} &= 1 - \frac{t - t_\mathrm{off}}{t_\mathrm{fall}} \end{align*} 
def pulse_with_tr_tf(t, t0, t_rise, t_fall, width):
    if t0 <= t < t0 + t_rise:
        return (t - t0) / t_rise
    if t0 + t_rise <= t < t0 + t_rise + width:
        return 1
    if t0 + t_rise + width <= t < t0 + t_rise + width + t_fall:
        return 1 - (t - (t0 + t_rise + width)) / t_fall
    return 0

良い点としてはステップ関数型とは違い立ち上がり立下り時間を考慮できています。しかし、立ち上がり開始・終了、立ち下がり開始・終了で傾き（1階微分）が不連続になります。場合によっては悪影響を及ぼす可能性があります。

線形での立ち上がりパルス

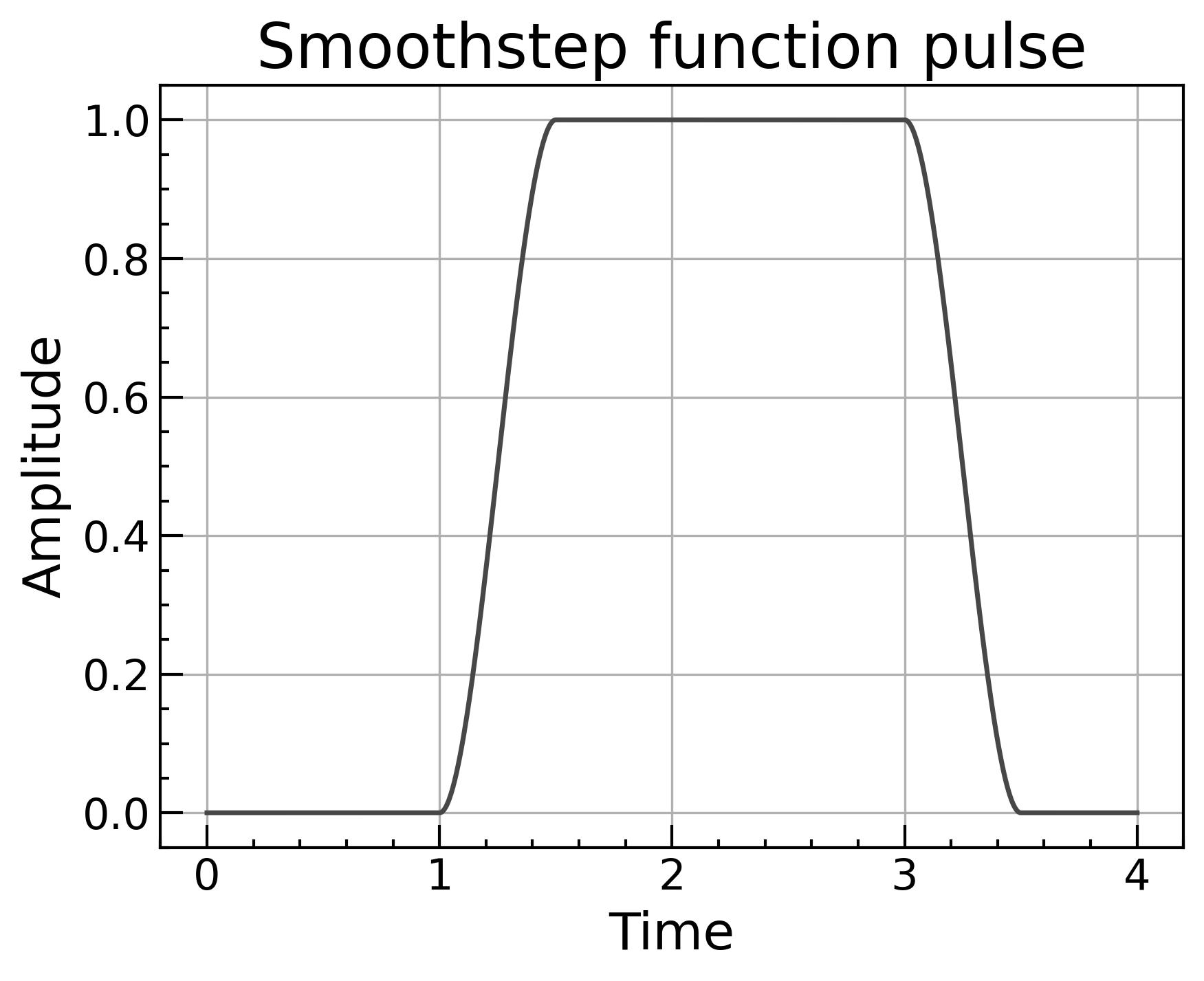
3. 1階微分までなめらかにしたい時

3.1 smoothstep型

[0,1][0, 1]で3x2−2x33x^2 - 2x^3を使う形。端点で傾きが0になるので接続が自然になります。 多項式で計算できるので後で紹介するものよりも計算が簡単です。

f(t)rise=3(t−tontrise)2−2(t−tontrise)3f(t)fall=1−(3(t−tofftfall)2−2(t−tofftfall)3)\begin{align*} f(t)_\mathrm{rise} &= 3\left( \frac{t - t_\mathrm{on}}{t_\mathrm{rise}} \right)^2 - 2\left( \frac{t - t_\mathrm{on}}{t_\mathrm{rise}} \right)^3 \\ f(t)_\mathrm{fall} &= 1 - \left( 3\left( \frac{t - t_\mathrm{off}}{t_\mathrm{fall}} \right)^2 - 2\left( \frac{t - t_\mathrm{off}}{t_\mathrm{fall}} \right)^3 \right) \end{align*} 
def smoothstep_pulse(t, t0, t_rise, t_fall, width):
    if t0 <= t < t0 + t_rise:
        x = (t - t0) / t_rise
        return 3*x**2 - 2*x**3
    if t0 + t_rise <= t < t0 + t_rise + width:
        return 1
    if t0 + t_rise + width <= t < t0 + t_rise + width + t_fall:
        x = (t - (t0 + t_rise + width)) / t_fall
        return 1 - (3*x**2 - 2*x**3)
    return 0

より高次の多項式バージョンもあるようです。参考: Wikipedia Smoothstep

smoothstep型のパルス

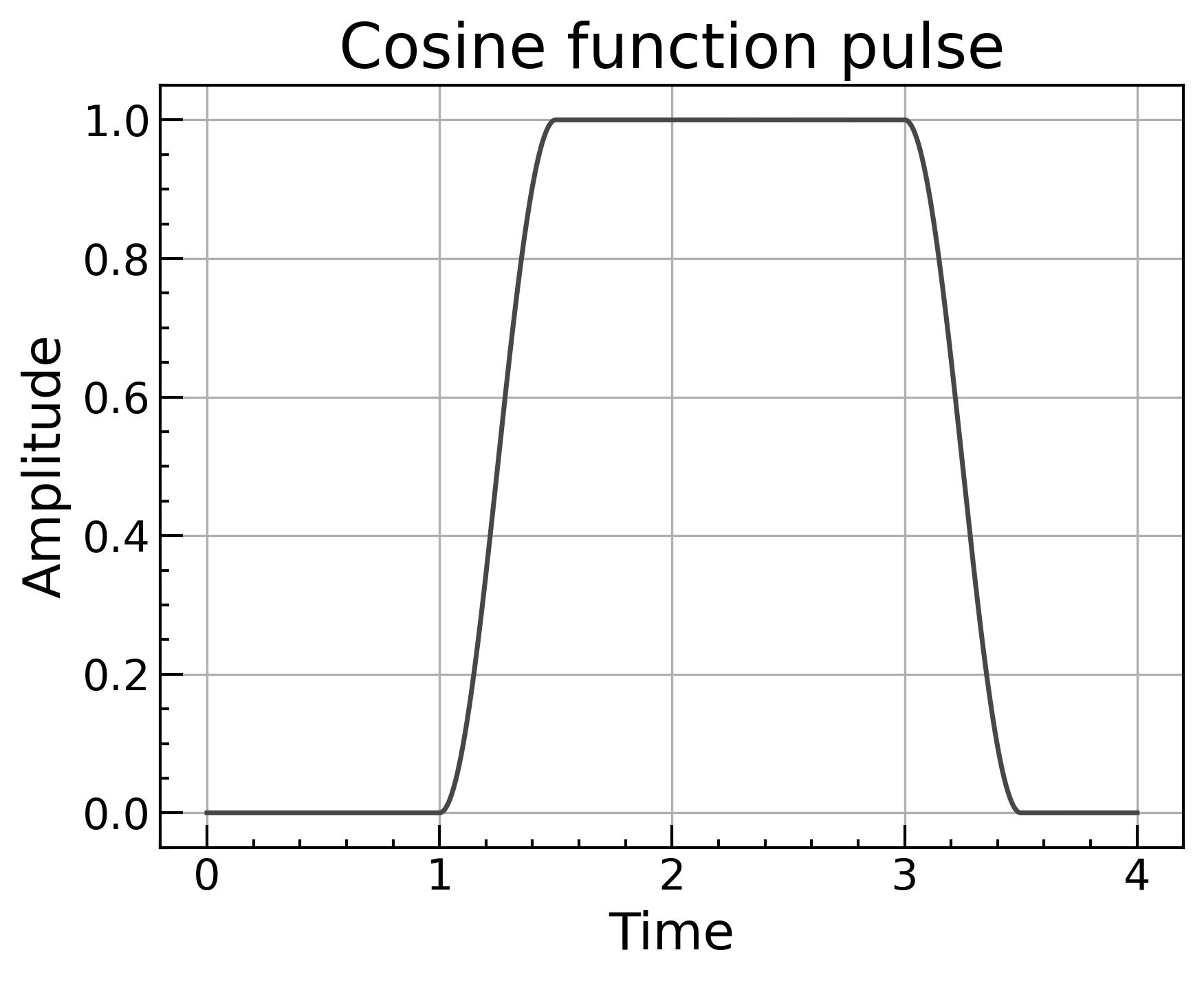
3.2 cos型

コサインを半周期だけ使うやり方です。こちらも端点の傾きが0になるので繋がりが滑らかです。

f(t)rise=12(1−cos⁡(πt−tontrise))f(t)fall=12(1+cos⁡(πt−tofftfall))\begin{align*} f(t)_\mathrm{rise} &= \frac{1}{2}\left( 1 - \cos\left( \pi\frac{t-t_\mathrm{on}}{t_\mathrm{rise}} \right) \right) \\ f(t)_\mathrm{fall} &= \frac{1}{2}\left( 1 + \cos\left( \pi\frac{t-t_\mathrm{off}}{t_\mathrm{fall}} \right) \right) \end{align*} 

def cos_pulse(t, t0, t_rise, t_fall, t_width):
    if t0 <= t < t0 + t_rise:
        return (1 - cos(pi * (t - t0) / t_rise)) / 2
    if t0 + t_rise <= t < t0 + t_rise + t_width:
        return 1
    if t0 + t_rise + t_width <= t < t0 + t_rise + t_width + t_fall:
        return (1 + cos(pi * (t - (t0 + t_rise + t_width)) / t_fall)) / 2
    return 0

cos型のパルス

4. 任意階微分が連続な波形

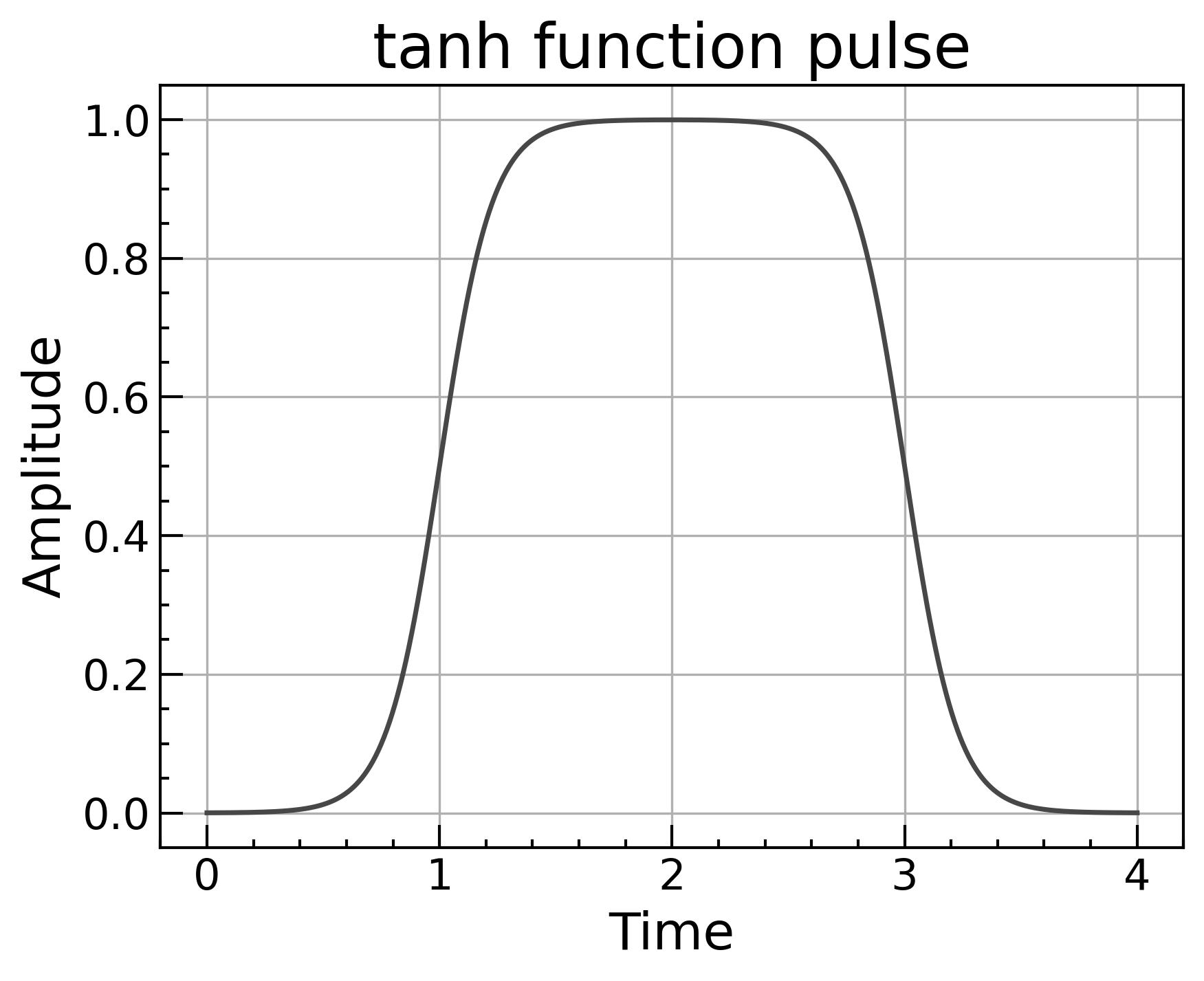
4.1 tanh型

f(t)=12(tanh⁡t−tonτrise−tanh⁡t−toffτfall)f(t) = \frac{1}{2}\left( \tanh{\frac{t - t_\mathrm{on}}{\tau_\mathrm{rise}}} - \tanh{\frac{t - t_\mathrm{off}}{\tau_\mathrm{fall}}} \right)

tanhは無限回微分可能でなめらかです。

この波形では滑らかに0と1を漸近的に行き来します。そのため、f(t)=0f(t) = 0やf(t)=1f(t) = 1に到達する有限の時刻は存在しません。 そこで、立ち上がり時間を「ピーク値の10%から90%に達するまでの時間」、立ち下り時間を「ピーク値の90%から10%に到達するまでの時間」と定義します。

以下では十分に長いパルスを前提にします。

パルスの立ち上がり前の時間、すなわち立ち上がりが始まる十分前t≪tofft \ll t_\mathrm{off}には

tanh⁡t−toffτfall≈−1\tanh{\frac{t - t_\mathrm{off}}{\tau_\mathrm{fall}}} \approx - 1

と近似できるので、f(x)f(x)は

f(t)≈12(tanh⁡(t−tonτrise)+1)f(t) \approx \frac{1}{2}\left( \tanh{\left( \frac{t - t_\mathrm{on}}{\tau_\mathrm{rise}} \right)} + 1 \right)

となります。

ここで、0<f(t)<10 < f(t) < 1であるので、任意の割合p∈(0,1)p \in (0, 1)を用いて式を変形すると、

p=12(tanh⁡(t−tonτrise)+1)2p−1=tanh⁡(t−tonτrise)\begin{align*} p &= \frac{1}{2}\left( \tanh{\left( \frac{t - t_\mathrm{on}}{\tau_\mathrm{rise}} \right)} + 1 \right) \\ 2p - 1 &= \tanh{\left( \frac{t - t_\mathrm{on}}{\tau_\mathrm{rise}} \right)}\\ \end{align*}

tanh⁡\tanhの逆関数は12ln⁡1+x1−x\frac{1}{2}\ln\frac{1+x}{1-x}であるので、

12ln⁡p1−p=t−tonτrise\frac{1}{2}\ln{\frac{p}{1-p}} = \frac{t-t_\mathrm{on}}{\tau_\mathrm{rise}}

ピーク時の10%、すなわちp=0.1p = 0.1の時刻tst_{s}は、

12ln⁡19=ts−tonτrisets=τrise2ln⁡19+ton\begin{align*} \frac{1}{2}\ln{\frac{1}{9}} &= \frac{t_{s}-t_\mathrm{on}}{\tau_\mathrm{rise}} \\ t_{s} &= \frac{\tau_\mathrm{rise}}{2}\ln{\frac{1}{9}} + t_\mathrm{on} \end{align*}

ピーク時の90%、すなわちp=0.9p = 0.9の時刻tet_{e}は、

12ln⁡9=te−tonτrisete=τrise2ln⁡9+ton\begin{align*} \frac{1}{2}\ln{9} &= \frac{t_{e}-t_\mathrm{on}}{\tau_\mathrm{rise}} \\ t_{e} &= \frac{\tau_\mathrm{rise}}{2}\ln{9} + t_\mathrm{on} \end{align*}

よって、立ち上がり時間は

te−ts=(τrise2ln⁡9+ton)−(τrise2ln⁡19+ton)=τriseln⁡9\begin{align*} t_{e} - t_{s} &= \left( \frac{\tau_\mathrm{rise}}{2}\ln{9} + t_\mathrm{on}\right) - \left( \frac{\tau_\mathrm{rise}}{2}\ln{\frac{1}{9}} + t_\mathrm{on} \right) \\ &= \tau_\mathrm{rise} \ln{9} \end{align*}

同様に立下りでは立ち上がり時間の十分後t≪tont \ll t_\mathrm{on}である時、

tanh⁡t−tonτrise≈1\tanh{\frac{t - t_\mathrm{on}}{\tau_\mathrm{rise}}} \approx 1

であるので

f(t)≈12(1−tanh⁡t−toffτfall)f(t) \approx \frac{1}{2}\left( 1 - \tanh{\frac{t - t_\mathrm{off}}{\tau_\mathrm{fall}}} \right)

となるので同じ手順で

tfall=τfallln⁡9t_\mathrm{fall} = \tau_\mathrm{fall}\ln{9}

と求めることができます。

まとめると、

  • 立ち上がり時間 : τriseln⁡9\tau_\mathrm{rise}\ln{9}
  • 立ち下がり時間 : τfallln⁡9\tau_\mathrm{fall}\ln{9}

tanh型のパルス

sigmoid型

f(t)=11+exp⁡(−τrise(t−ton))−11+exp⁡(−τfall(t−toff))f(t) = \frac{1}{1 + \exp{(-\tau_\mathrm{rise}(t - t_\mathrm{on}))}} - \frac{1}{1 + \exp{(-\tau_\mathrm{fall}(t - t_\mathrm{off}))}}

tanh型と同様にf(t)=0f(t) = 0やf(t)=1f(t) = 1に到達する有限の時刻は存在しません。そのため先ほどと同様の定義でパルスの立ち上がり、立ち下がり時間を求めます。

t≪tofft \ll t_\mathrm{off}の時、

11+exp⁡(−τfall(t−toff))≈0\frac{1}{1 + \exp{(-\tau_\mathrm{fall}(t - t_\mathrm{off}))}} \approx 0

よって、

f(t)≈11+exp⁡(−τrise(t−ton))f(t) \approx \frac{1}{1 + \exp{(-\tau_\mathrm{rise}(t - t_\mathrm{on}))}}

0<f(t)<10 < f(t) < 1なのでp∈(0,1)p \in(0,1)を用いて変形すると、

p=11+exp⁡(−τrise(t−ton))1−pp=exp⁡(−τrise(t−ton))ln⁡1−pp=−τrise(t−ton)\begin{align*} p &= \frac{1}{1 + \exp{(-\tau_\mathrm{rise}(t - t_\mathrm{on}))}} \\ \frac{1 - p}{p} &= \exp(-\tau_\mathrm{rise}(t - t_\mathrm{on})) \\ \ln{\frac{1-p}{p}} &= -\tau_\mathrm{rise}(t - t_\mathrm{on}) \end{align*}

ピーク時の10%、すなわちp=0.1p = 0.1の時刻tst_sは

ln⁡9=−τrise(ts−ton)ts=−ln⁡9τrise+ton\begin{align*} \ln{9} &= -\tau_\mathrm{rise}(t_s - t_\mathrm{on})\\ t_s &= -\frac{\ln{9}}{\tau_\mathrm{rise}} + t_\mathrm{on} \end{align*}

ピーク時の90%、すなわちp=0.9p = 0.9の時刻tet_eは

−ln⁡9=−τrise(te−ton)te=ln⁡9τrise+ton\begin{align*} -\ln{9} &= -\tau_\mathrm{rise}(t_e - t_\mathrm{on})\\ t_e &= \frac{\ln{9}}{\tau_\mathrm{rise}} + t_\mathrm{on} \end{align*}

立ち上がり時間は

trise=ln⁡9τrise+ton−(−ln⁡9τrise+ton)=2ln⁡9τrise\begin{align*} t_\mathrm{rise} &= \frac{\ln{9}}{\tau_\mathrm{rise}} + t_\mathrm{on} - \left( -\frac{\ln{9}}{\tau_\mathrm{rise}} + t_\mathrm{on} \right) \\ &= 2\frac{\ln{9}}{\tau_\mathrm{rise}} \end{align*}

立ち下がり時間はt≫tont \gg t_\mathrm{on}において、

11+exp⁡(−τrise(t−ton))≈1\frac{1}{1 + \exp{(-\tau_\mathrm{rise}(t - t_\mathrm{on}))}} \approx 1

となるので

f(t)=1−11+exp⁡(−τfall(t−toff))f(t) = 1 - \frac{1}{1 + \exp{(-\tau_\mathrm{fall}(t - t_\mathrm{off}))}}

同じ手順で求めることができる

tfall=2ln⁡9τfallt_\mathrm{fall} = 2\frac{\ln{9}}{\tau_\mathrm{fall}}

まとめると、

  • 立ち上がり時間 : 2ln⁡9τrise2\frac{\ln{9}}{\tau_\mathrm{rise}}
  • 立ち下がり時間 : 2ln⁡9τfall2\frac{\ln{9}}{\tau_\mathrm{fall}}

Sigmoid型とtanh型のパルスの形状は同じになります。

sigmoid型のパルス

まとめ

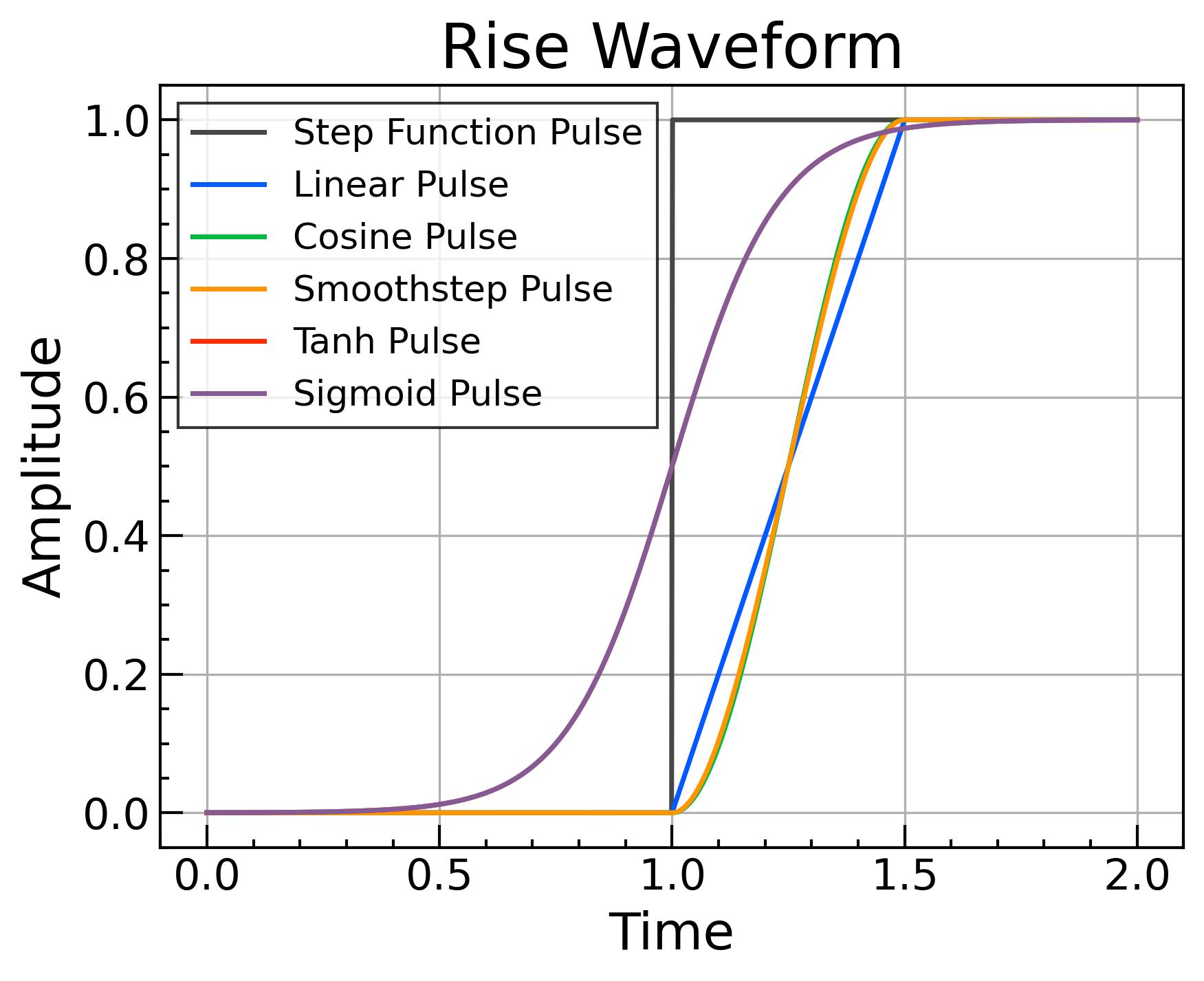
  • 手早く試すなら：線形型
  • 傾きの段差をなくすなら： cosかsmoothsteps
  • 滑らかさが重要なら：tanhかsigmoid

各パルスの立ち上がり

紹介したパルスの立ち上がり方をまとめました。

各パルスの立ち上がり方の比較

書いた人

profile_image

お茶の葉

物理とプログラミングが好きな人