LLG方程式とPythonによる簡単なシミュレーション

投稿日：2025/07/18 更新日:2025/07/18

LLG方程式とは

磁性体における磁化の時間発展を記述する方程式として、Landau-Lifshitz-Gilbert (LLG) 方程式があります。 LLG法手式は以下のように示されます。

\frac{d\bm{M}}{dt} = -\gamma\bm{M}\times\bm{H}_{eff} + \frac{\alpha}{M_s}\bm{M}\times\frac{\bm{M}}{dt}

ここで、

$\bm{M}$ : 磁化ベクトル
$\bm{H}_{eff}$ : 有効磁場
$\gamma$ : 磁気回転比
$\alpha$ : 減衰定数
$M_s$ : 飽和磁化

数値解析や理論解析ではしばしば磁化を正規化した単位ベクトル $\bm{m} = \bm{M}/M_s$ を用います。これによりLLG方程式は次のようになります。

\frac{d\bm{m}}{dt} = -\gamma\bm{m}\times\bm{H}_{eff} + \alpha\bm{m}\times\frac{d\bm{m}}{dt}

右辺の微分項の除去

このままでは右辺に微分項が含まれているため、数値シミュレーションを行うには不都合です。微分項を除去した形に式を変形します。

まず、右辺の $\tfrac{d\bm{m}}{dt}$ に自身を代入します。

\frac{d\bm{m}}{dt} = -\gamma\bm{m}\times\bm{H}_{eff} + \alpha\bm{m} \times \left( -\gamma\bm{m}\times\bm{H}_{eff} + \alpha\bm{m}\times\frac{d\bm{m}}{dt} \right)

これを展開すると

\frac{d\bm{m}}{dt} = -\gamma\bm{m}\times\bm{H}_{eff} -\alpha\gamma\bm{m}\times(\bm{m}\times\bm{H}_{eff}) + \alpha^2\bm{m}\times \left(\bm{m}\times\frac{d\bm{m}}{dt} \right)

ここで、ベクトル三重積の公式より第３項の部分は

\bm{A} \times (\bm{B} \times \bm{C}) = (\bm{A}\cdot\bm{C})\bm{B} - (\bm{A}\cdot\bm{B})\bm{C}

を使って第３項を変形します

\bm{m}\times \left(\bm{m}\times\frac{d\bm{m}}{dt} \right)　＝ \left(\bm{m} \cdot \frac{d\bm{m}}{dt}\right)\bm{m} - (\bm{m}\cdot\bm{m})\frac{d\bm{m}}{dt}

特に $\bm{m}$ は単位ベクトル( $|\bm{m}| = 1$ )なので

\bm{m}\cdot\bm{m} = 1, \; \frac{d}{dt}(\bm{m}\cdot\bm{m}) = 2\bm{m}\cdot\frac{d\bm{m}}{dt} = 0

より、

\bm{m}\cdot\frac{d\bm{m}}{dt} = 0

これを用いると、

\bm{m}\times \left(\bm{m}\times\frac{d\bm{m}}{dt} \right) = -\frac{d\bm{m}}{dt}

となります。ここまででLLG方程式は次のように変形されます。

\frac{d\bm{m}}{dt} = -\gamma\bm{m}\times\bm{H}_{eff} -\alpha\gamma\bm{m}\times(\bm{m}\times\bm{H}_{eff}) - \alpha^2 \frac{d\bm{m}}{dt}

となっています。微分を左辺に持っていくと、

(1+\alpha^2)\frac{d\bm{m}}{dt} = -\gamma\bm{m}\times\bm{H}_{eff} -\alpha\gamma\bm{m}\times(\bm{m}\times\bm{H}_{eff})

整理すると、

\frac{d\bm{m}}{dt} = -\frac{\gamma}{1+\alpha^2} \bm{m}\times\bm{H}_{eff} -\frac{\gamma\alpha}{1 + \alpha^2}\bm{m}\times(\bm{m}\times\bm{H}_{eff})

これにより右辺から微分を取り除くことができました。

Pythonでシミュレーションしてみる

ここでは上記で導出した式をPythonでシミュレーションしてみましょう。SciPyの solve_ivp を使って時間発展を計算します。

以下はPythonのコードです。

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
from math import sin, cos, radians

# 定数
GAMMA_E =  1.760_859_627_84e11 # gyromagnetic ratio of electron [s^-1 T^-1]
NANO = 1e-9

# h_eff [T]
def precession_torque(m, h_eff):
    return -GAMMA_E * np.cross(m, h_eff)

# h_eff [T]
def damping_torque(m, h_eff, alpha):
    return -alpha*GAMMA_E * np.cross(m, np.cross(m, h_eff))

# hext: 外部磁場 [T]
def llg(t, m, hext, alpha):
    total_heff = hext

    dm_dt = precession_torque(m, total_heff) + damping_torque(m, total_heff, alpha)

    return 1 / (1 + alpha*alpha) * dm_dt

def main():
    # 計算を行う時間のリストを作成
    t_list = np.linspace(0, 1 * NANO, 1000)

    # 外部磁場の設定
    hext = np.array([0, 0, 0.5]) # T
    # 減衰定数の設定
    alpha = 0.05

    # 初期磁化の設定
    theta = radians(45)
    phi = radians(0)
    m_init = np.array([sin(theta)*cos(phi), sin(theta)*sin(phi), cos(theta)])

    # 数値計算の実行
    result = solve_ivp(llg, (t_list[0], t_list[-1]), m_init, t_eval = t_list, args = (hext, alpha))

    # == 計算結果をプロット ==
    mx = result.y[0]
    my = result.y[1]
    mz = result.y[2]

    fig = plt.figure(layout = 'tight')
    # 3D軌道をプロット
    ax = fig.add_subplot(111, projection = '3d')
    ax.plot(mx, my, mz, marker = '')
    ax.set_xlabel('m_x')
    ax.set_ylabel('m_y')
    ax.set_zlabel('m_z')
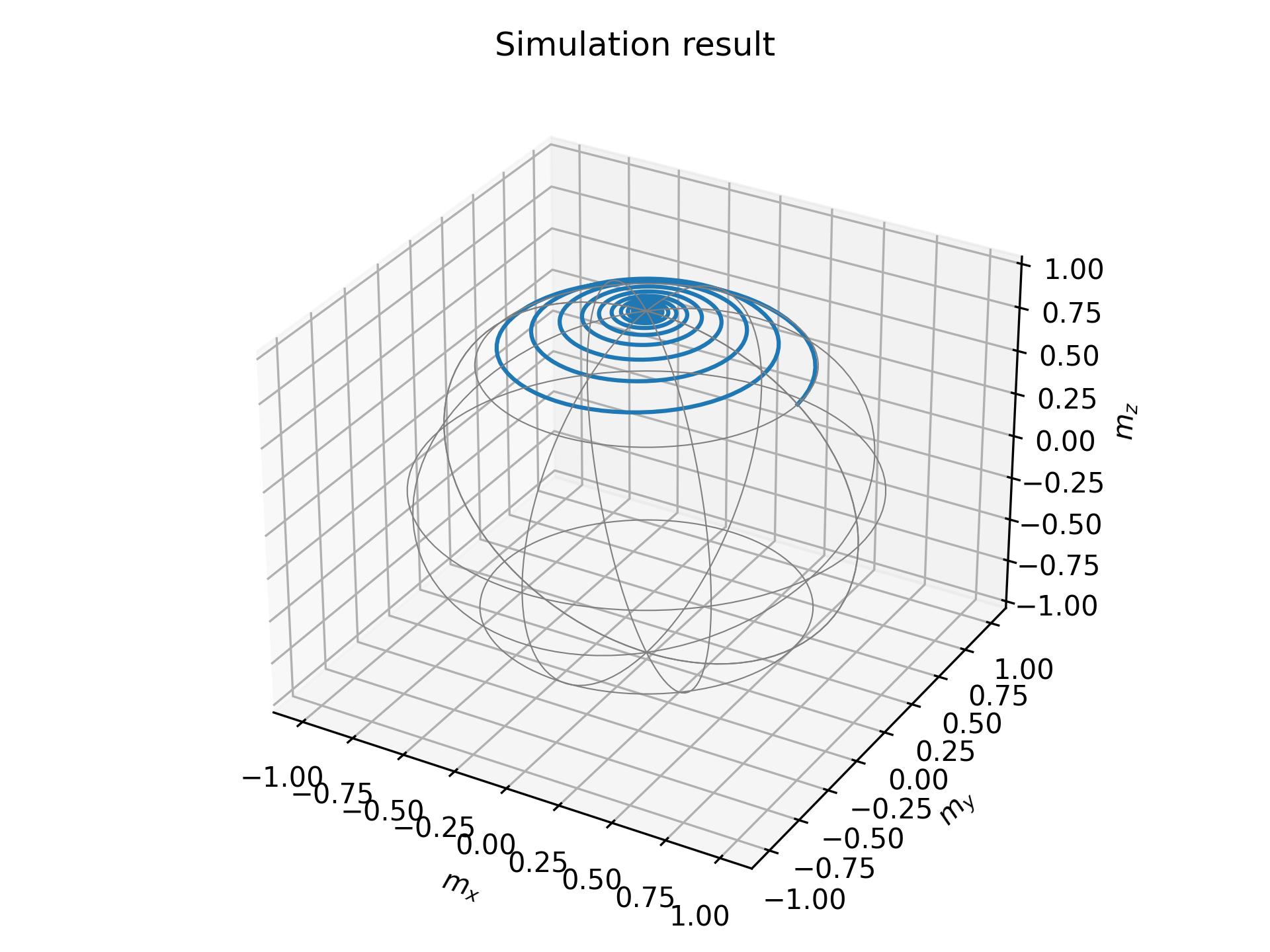
    ax.set_title('Simulation result')

    # 補助線を描画
    for theta in np.linspace(0, np.pi, 5):
        r = np.sin(theta)
        lin = np.linspace(0, 2*np.pi, 100)
        ax.plot(r*np.cos(lin), r*np.sin(lin), np.cos(theta), color = 'gray', marker = '', linewidth = 0.5)
    for theta in np.linspace(0, np.pi, 5):
        lin = np.linspace(0, 2*np.pi, 100)
        ax.plot(np.cos(theta)*np.sin(lin), np.sin(theta)*np.sin(lin), np.cos(lin), color = 'gray', marker = '', linewidth = 0.5)

    fig.savefig('simulation_result.jpg', dpi = 300)

if __name__ == '__main__':
    main()

このシミュレーションでは、磁化が歳差運動しながら、z方向に印加された外部磁場に徐々に揃っていく様子が確認できます。これは、歳差項によって磁化が回転運動しつつ、ダンピング項の効果で徐々に外部磁場方向へ収束していく典型的な挙動です。

シミュレーション結果