Diffie-Hellman鍵交換の計算方法

Diffie-Hellman鍵交換とは

ディフィー・ヘルマンと読みます。

鍵配送問題を解決する手法です。盗聴者に知られても大丈夫な数を交換することにより、共通の鍵を作りだします。

アルゴリズム

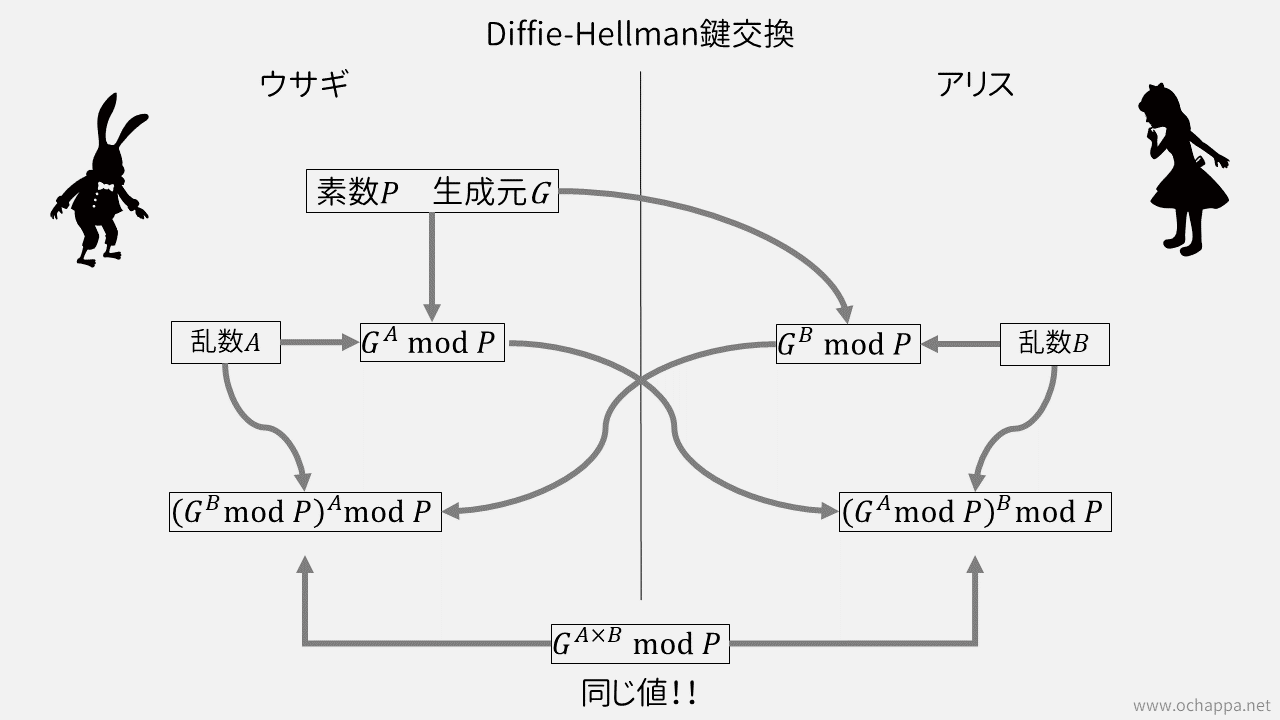
ウサギとアリスが鍵交換する場面を考えます。

1. ウサギが大きな素数$P$と生成元$G$を送信します。
   生成元については後から説明します。
2. ウサギは$1 \leqq A \leqq P-2$の範囲で整数$A$をランダムに選びます。
3. アリスは$1 \leqq B \leqq P-2$の範囲で整数$B$をランダムに選びます。
4. ウサギはアリスに$G^A \mod P$という数を送信します。
5. アリスはウサギに$G^B \mod P$という数を送信します。
6. ウサギは送られた数と自身の数$A$で$(G^B \mod P)^A \mod P$を計算する。
7. アリスは送られた数と自身の数$B$で$(G^A \mod P)^B \mod P$を計算する。

$P$は非常に大きな素数であることが望ましいです。

生成元について

生成元とは、$x^1, ..., x^{p-1} \mod P$の値がすべて異なる$x$のことです。

例

素数$P = 5$として$G^a \mod P$を考えます。

$G^a \mod P$の値を表にまとめました

$G = 2, 3$の時$G^a \mod P$の値がすべて異なっています。したがって、$P=5$の時の生成元は$2, 3$であることが分かります。

実際に計算する

1. $P$と$G$を決める

今回は$P = 11$とします。 生成元は$2,6,7,8$といくつかあります。今回は$G = 7$とします。

2. $A$を決める

$1 \leqq A \leqq P-2$の範囲から$A$を選びます。
$1 \leqq A \leqq 9$なので、$A = 2$とします。

3. $B$を決める

$1 \leqq B \leqq P-2$の範囲から$B$を選びます。
$1 \leqq B \leqq 9$なので、$B = 9$とします

4. $G^A \mod P$を求める

計算します。

$7^2 \mod 11 = 5$

5. $G^B \mod P$を求める

計算します。

$7^9 \mod 11 = 8$

6. $(G^B \mod P)^A \mod P$を求める

$G^B \mod P$は手順（5）で求めたのでその値を使います。

$8^2 \mod 11 = 9$

7. $(G^A \mod P)^B \mod P$を求める

$G^A \mod P$は手順（4）で求めたのでその値を使います。

$5^9 \mod 11 = 9$

手順（6）、（7）で求めた値が一致しています！
共通鍵を生成することができました😄

なぜ盗聴者は鍵を盗めないのか？

通信を盗聴したときに得られる情報は以下の4つです。

$P, G, G^A \mod P, G^B \mod P$

これらの情報から鍵である$G^{A \times B} \mod P$を容易に計算できるでしょうか？

$G^A \mod P$から$A$が求まれば手順（6）のようにして秘密鍵を計算できますが、実際には難しいことが知られています。

離散対数問題と言って$G^x \mod P$から$x$を効率よく計算するアルゴリズムはまだ見つかっていません。
離散対数問題の難しさがこの鍵交換アルゴリズムの強度となります。

参考文献

結城浩（2015）暗号技術入門　第3版